Balanced Lineup

ST表

设f[i,j]表示从第i个元素到2^j^个元素的最值

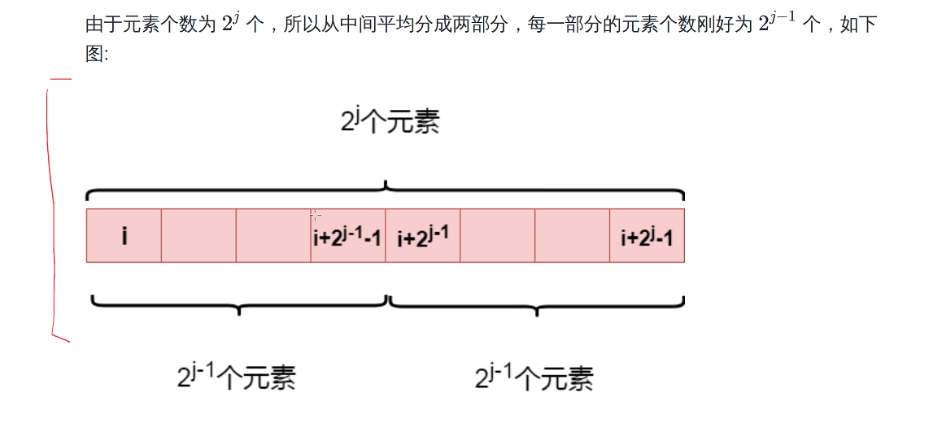
状态转移方程：f[i,j]=max(f[i,j-1],f[i+2^j-1^,j-1])

边界条件：f[i,0]=a[i];

查询：

对于查询区间[L,R]，令x满足2^x^<=R-L+1的最大整数，即x=int(log(R-l+1)/log(2))

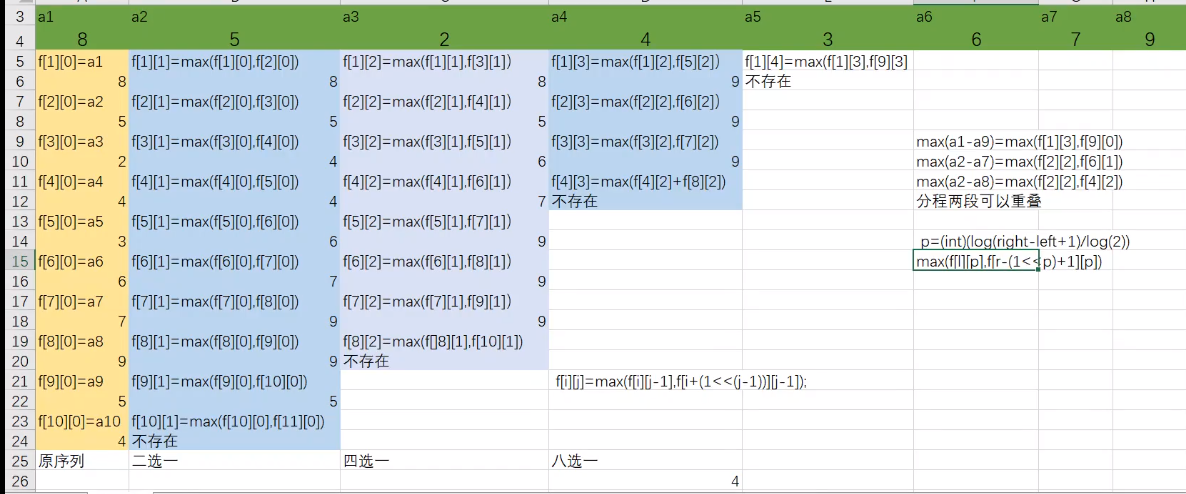
Balanced Lineup

#include <iostream>
#include <algorithm>
using namespace std;
int f[50010][20];
int g[50010][20];
int main()
{
    int t,n,q,x,y;
    cin>>n>>q;
    for(int i=1;i<=n;i++)
    {
        cin>>t;
        f[i][0]=t;
        g[i][0]=t;
    }
    for(int i=1;(1<<i)<=n;i++)
        for(int j=1;(j+(1<<i)-1)<=n;j++)//j+(1<<i)-1<=n最后一个值要在原数组内
        {
            f[j][i]=max(f[j][i-1],f[j+(1<<(i-1))][i-1]);//2的i次方的区间的最值为前2的i次方-1区间的最值与后2的i次方-1区间最值的最值
            g[j][i]=min(g[j][i-1],g[j+(1<<(i-1))][i-1]);
        }
    while(q--)
    {
        cin>>x>>y;
        int z=0;
        while(1<<(z+1)<=y-x+1)//计算区间长度于2ˆz的关系，用小于2^z<=y-x+1，的 z 把区间分成可以交叉的两部分x 到 x+2^（k）- 1, 到 y -(y-x+1<<k)+1 到 y 的两部分
            z++;
        int ans=max(f[x][z],f[y-(1<<z)+1][z])-min(g[x][z],g[y-(1<<z)+1][z]);
        cout<<ans<<endl;
    }
    return 0;
}