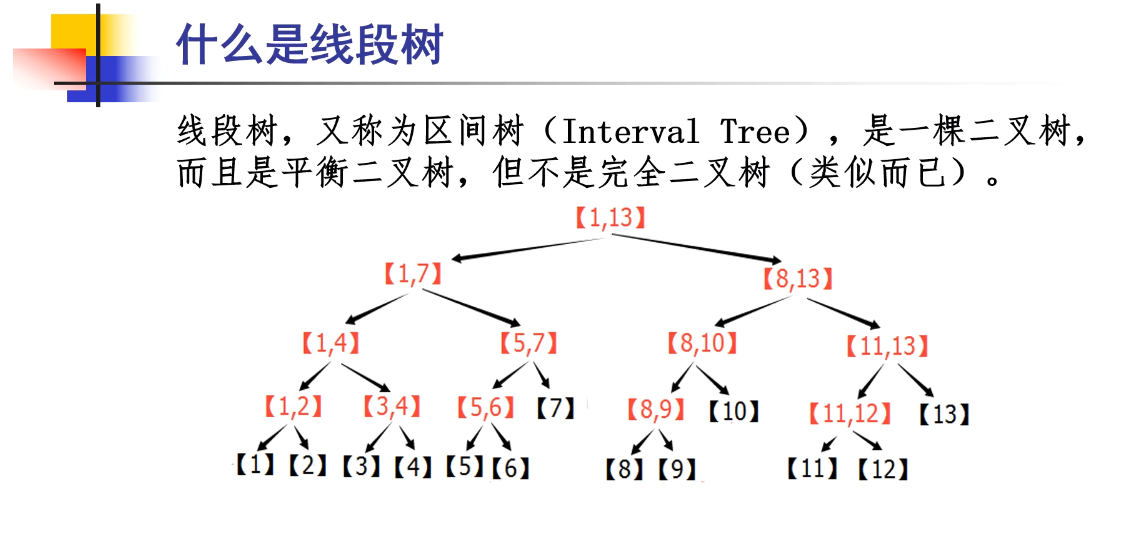
树状数组

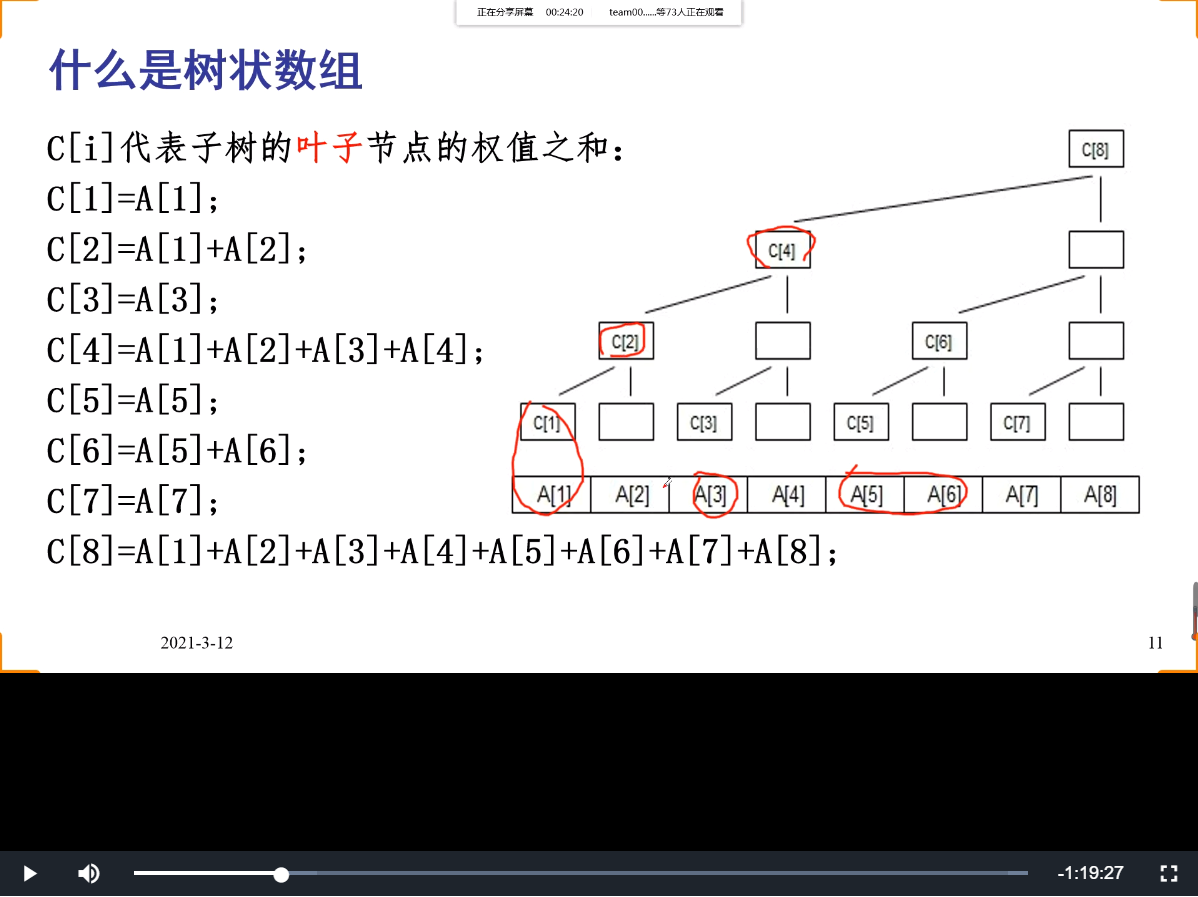
lowbit

lowbit（）函数用来取一个二进制最低位的一与后边的0组成的数

例：5（101），lowbit（5）=1（1）

​ 12（1100），lowbit（12）=4（100）

1
2
3
4

int lowbit(int t)
{
    return t&(-t);
}

原理，二进制数的负数是正数取反加一

12（1100），-12（0100）

求逆序数对

基本思想:开一个数组c[n+1],初始化为0，记录前面数据的出现情况;当数据a出现时，就令c[a]=1。这样的话，若求a的逆序数，只需要算出在当前状态下c[a+1,n]中有多少个1，因为这些位置的数在a之前出现且比a大。==复杂度O(n^2)==

树状数组的经典应用

另开一个==树状数组d[n+1]==,初始化为0，d[i]记录i结点所==管辖范围内==当前状态有多少个数;
当添加数据a时，就向上更新d数组,这样，当求a的逆序数时，只需要算sum(n)-sum(a)即可;

“区间修改+单点查询”的树状数组

基本思想：通过“差分”的方法（数组中记录的是每个元素与前一个元素的差），把问题转化为常规树状数组！

1

若原数组为a[i],设数组d[i]=a[i]-a[i-1](a[0]=0),则可以通过求d[i]的前缀和实现单点查询a[i]。

区间修改

当给区间[1,r]加上x的时候，a[1]与前一个元素a[l-1]的差增加了x，a[r+1]与a[r]的差减少了x。根据d[i]数组的定义，只需给d[l]加上x，给d[r+1]减去x即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

//单点更新“差分”，为区间修改做准备(c是树状数组)
void add(int p,int x)
{
	while(p<=n)
	c[p]+=x,p+=p&-p;
}
//区间修改（通过两个端点的更新，实现区间修改的目的）
void range_add(int r,int x)
{
	add(l,x),add(r+1,-x);
}
//单点查询（因为差分，所以单点值即前缀和）
int ask(int p)
{
	int res=0;
	while(p)
	res+=c[p],p-=p&-p;
	return res;
}

“区间修改+区间查询”的树状数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

//维护2个树状数组
void add(int p,int x)
{
	for(int i=p;i<=n;i+=i&-i)
	c1[i]+=x,c2[i]+=x*p;
}
//区间修改（通过两个端点的更新，实现区间修改的目的）
void range_add(int r,int x)
{
	add(l,x),add(r+1,-x);
}
int range_ask(int l,int r)
{
    return ask(r)-ask(l-1);
}

B - Minimum Inversion Number

思路：

首先是怎么求其中一个序列的逆序数对

假设序列开始一个数都没有

每添加一个数之前计算序列有多少数大于该数（即在该位添加时会增加多少对逆序数）<===算作一个状态

将所有状态相加即是该序列的逆序数对数量

拿样例来说

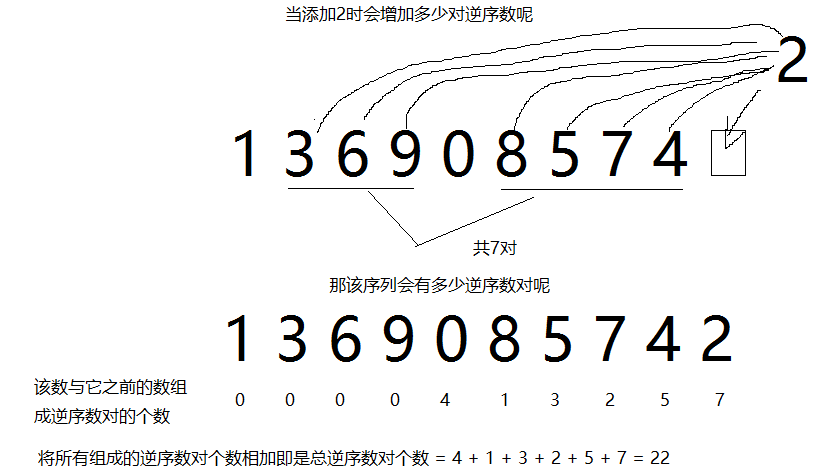
当a0移动到an-1末尾后减少了它之后能与它形成逆序数对的个数(比它小的数)

​ 增加了在末尾时它之前能与它形成逆序数对的个数(比它大的数)

由于下一个循环数列必定是将头移至尾，所以减少的个数为比它小的个数，增加的个数为比它大的个数

因为数是不会重复的且为0~n-1共n个，所以 a[i] - 1就是序列中比它小的数的个数，n - a[i]就是序列中比它大的数的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int tree[6000],a[6000];
int n;

 int lowbit(int t)
{
    return t&(-t);
}
void add(int x,int d) {
    while(x<=n) {
        tree[x]+=d;
        x+=lowbit(x);
    }
}

int sum(int x) {
    int ans = 0;
    while(x>0) {
        ans+=tree[x];
        x-=lowbit(x);
    }

    return ans;
}

int main() {
    while(cin>>n) {
        int cnt=0;
        memset(tree,0,sizeof(tree));
        for(int i=1;i<=n;i++) {
            scanf("%d",&a[i]);
            a[i]++;//树状数组从1开始 数据范围(0~n-1)
            cnt+=sum(n)-sum(a[i]);//找出所有比a[i]大的数的逆序数对数
            add(a[i],1);//记录这个数
        }

        int ans = cnt;
        for(int i=1;i<=n;i++) {
            cnt = cnt - a[i] + n - a[i] + 1;//比较完后因为 n 个数范围(0~n-1)且不重复， 所以比a[i] 小的数为a[i]-1;
             // 每次将头元素移至末尾都会减少比头小的数(a[i] - 1)个逆序数，增加比头大的数(n - a[i])个逆序数
             // 所以增加的逆序数为 n - a[i] * 2 + 1  [+(n - a[i]) -(a[i] - 1)]
            ans = min(ans,cnt);
        }

        printf("%d\n",ans);
    }

return 0;
}

线段树构造

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

//PushUp函数更新节点信息，这里以求和为例
void PushUp(int rt)
{
	SegTree[rt].val=SegTree[re<<1].val+SegTree[re<<1|1].val;
}
void build(int l,int r,int rt)
{
	if(l==r)
	{
		SegTree[rt].val=A[l];
		return;
	}
	int m=(l+r)/2;
	build(l,m,rt*2);//递归构造左子树
	build(m+1,r,rt*2+1);//右子树
	PushUp(rt);//回溯，向上更新
}

单点更新（A[l]+=C）

1
2
3
4
5
6
7
8
9
10
11
12
13
14

//l,r表示当前节点区间，rt表示当前线段树的根节点编号
void Update(int L,int C,int r,int rt)
{
    if(l==r)
    {
        SegTree[rt].val+=C;
        return;
    }
    int m=(l+r)>>1;
    if(L<=m)Update(L,C,l,m,rt<<1);
    else
        Update(L,C,m+1,r,rt<<1|1);
    PushUp(rt);
}

区间查询

1
2
3
4
5
6
7
8
9
10
11
12
13
14

（询问A[L..R]的和)

//[L,R]表示操作区间，[1,r]表示当前区间，rt表示当前节点编号
   int Query(int L,int R,int l,int r,int rt) {
if(L<= l && r<= R)
return SegTree[rt].val;//在区间内直接返回if(L > r llR< 1)
return 0;
int m = ( l + r ) >>1;
int ANS = 0;
if(L<=m)ANS+=Query(L,R,l,m,rt<<1);//左子区间与[L,R]有重叠，递归
if(R>m)ANS+=Query(L,R,m+1,r,rt<<1|1);//右子区间与[L,R]有重叠，递归
    return ANS;
// return Query(L,R,1,m,rt<<1) + Query(L,R,m+1,r,rt<<1| 1);

区间更新

​

A - Balanced Lineup

线段树模板题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <math.h>
using namespace std;
int t,n,q;
long tree1[50010<<2];
long tree2[50010<<2];
long a[50010];
void PushUp(int rt){
    tree1[rt] =max(tree1[rt*2] , tree1[rt*2+1]) ; //区间和的更新操作
    tree2[rt] =min(tree2[rt*2] , tree2[rt*2+1]) ;
}

void Build(int l,int r,int rt){
    // l,r 代表的是这个区间内的左端点 和 右端点， rt代表的是 [l,r] 这个区间内的值是存在哪一个位置的。
    if(l==r){
         tree1[rt] = a[l];
         tree2[rt] = a[l];
        return;
    }
    int m=(l+r)/2;// 对于区间区分，我们一般将m点划入左半边区间
    Build(l,m,rt*2);
    Build(m+1,r,rt*2+1);
    PushUp(rt); // PushUp 函数是通过2个子节点来更新现在这个节点的状态

}
long MAXQuery(int l,int r,int rt,int L,int R){// [L,R]为查询区间
    if(L <= l && r <= R){
        return tree1[rt];// 如果成立则满足查询区间覆盖了当前区间， 直接返回当前区间的值
    }
    int m=(l+r)/2;
    long res=0;
    if(L<=m)    res=max(res,MAXQuery(l,m,rt*2,L,R));//左边有一部分需要查询的区域。
    if(m<R)     res=max(res,MAXQuery(m+1,r,rt*2+1,L,R));//右边有一部分。
    return res;

}
long MINQuery(int l,int r,int rt,int L,int R){// [L,R]为查询区间
    if(L <= l && r <= R){
        return tree2[rt];// 如果成立则满足查询区间覆盖了当前区间， 直接返回当前区间的值
    }
    int m=(l+r)/2;
    long res=0x3f3f3f;
    if(L<=m)    res=min(res,MINQuery(l,m,rt*2,L,R));//左边有一部分需要查询的区域。
    if(m<R)     res=min(res,MINQuery(m+1,r,rt*2+1,L,R));//右边有一部分。
    return res;

}

int main()
{

        scanf("%d%d",&n,&q);
        for(int i = 1; i <= n; i++)
            scanf("%ld", &a[i]);
        Build(1,n,1);
        int a,b;
        while(q--){
            scanf("%d%d",&a,&b);
            cout << MAXQuery(1,n,1,a,b)-MINQuery(1,n,1,a,b) << endl;
        }
    return 0;
}

• 连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。

• 强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。

• 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。

• 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

  1.Kruskal算法

  此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。
  \1. 把图中的所有边按代价从小到大排序；
  \2. 把图中的n个顶点看成独立的n棵树组成的森林；
  \3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
  \4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

  2.Prim算法

  此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

  1. 图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;
  2. 在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。
  3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

  由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息。

  Bakery

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56

  #include<bits/stdc++.h> using namespace std; #define LL long long const int maxn = 1e5+7; int a[maxn]; int vis[maxn]; vector<pair<int,LL> >e[maxn];//pair是将2个数据组合成一组数据 int main() { int n,m,k;//城市，道路，仓库 LL ans = 1e18; cin>>n>>m>>k; for(int i = 1;i<=m;i++) { int u,v; LL w; scanf("%d%d%lld",&u,&v,&w); e[u].push_back(make_pair(v,w)); e[v].push_back(make_pair(u,w)); } if(!k) { cout<<-1<<endl; return 0; } else if(k==n) { cout<<-1<<endl; return 0; } for(int i = 1;i<=k;i++) scanf("%d",&a[i]),vis[a[i]]=1;//标记仓库 for(int u = 1;u<=n;u++) { // cout<<e[u].size(); if(vis[u])continue; for(int i = 0;i<e[u].size();i++) { int v = e[u][i].first;//找到与此点相连的点 LL w = e[u][i].second;//距离 // cout<<e[2][2].first; // cout<<e[2][2].second; // break; //cout<<v<<" "<<w<<endl; if(vis[v]) ans = min(ans,w); } } if(ans==1e18) cout<<-1<<endl; else cout<<ans<<endl; }

倍增法求LCA

暴力

首先把u,v中深度最大的结点提到和另一结点相同的深度，然后暴力一起向上，知道u=v为止。

祖先

对于一颗树的一个结点u ，她的爸爸的爸爸是她的祖先，她的爸爸的祖先也是她的祖先…..以此类推，直到根结点，根结点也是她的祖先。

公共祖先

对于一棵树的两个结点u, v,u,v的共同的祖先称作她们的公共祖先。

LCA

指u,v最近公共祖先，记为LCA(u, z)。最近公共祖先也就是u,v的公共祖先中最深的。

暴力相当于每次只跳2^0^步，而倍增通过从大到小枚举2的次幂，在枚举到每个i时会以下跳2^i^次，在倍增中只跳一次，暴力却需要2的i次方倍。

为什么i只需要20呢，因为y=2^x^的增长速度是指数级别。

2^17^=131072基本满足题目数据范围。

pog loves szh III

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
using namespace std ;
typedef long long LL ;
const int N = 400030 ;
const int DEG = 30 ;
int n;

struct Edge{
    int to,next;
}edge[N<<1];

int head[N],tot;

void add(int u,int v){//链式前向星
    edge[tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot++;
}



int fa[N][DEG] , deg[N];

void dfs(int u) {
    for(int i=head[u]; i!=-1; i=edge[i].next) {
        int to=edge[i].to;
        if(to==fa[u][0])
            continue;
        deg[to]=deg[u]+1;//深度信息储存
        fa[to][0]=u;
        dfs(to);
    }
}
void F()//i的2^j祖先就是i的（2^(j-1))祖先的2^(j-1)祖先
{
    for(int j=1; (1<<j)<=n; j++)
        for(int i=1; i<=n; i++)
            fa[i][j]=fa[fa[i][j-1]][j-1];
}

int LCA(int u,int v)
{
    if(deg[u] > deg[v])swap(u,v);
    int u1 = deg[u], v1 = deg[v];
    int u2 = u, v2 = v;
       int det = v1-u1;
   for( int i = 0 ;(1<<i)<=det;i++)
        if((1<<i)&det)
            v2 = fa[v2][i];
    if(u2 == v2)return u2;
    for(int i = DEG-1; i >= 0; i--)  //从最大祖先开始，判断a,b祖先，是否相同
    {
        if(fa[u2][i] == fa[v2][i])
            continue;
        u2 = fa[u2][i];            //如不相同，a b同时向上移动2^j
        v2 = fa[v2][i];
    }
    return fa[u2][0];              
}
void init(){
    tot = 0;
    memset(head,-1,sizeof(head));
}
int main()
{
    ios::sync_with_stdio(false);
    while(scanf("%d",&n)!=EOF){
        init();
        for( int i = 1 ; i < n ; ++i ) {
            int u , v ;
            cin>>u>>v;
            add( u , v ) ;
            add( v , u ) ;
        }
        dfs(1);
        F();
        int q ;
        cin>>q;
        while( q-- ) {
            int x , y ;
            scanf("%d%d",&x,&y);
           // cin>>x>>y;
            cout<<LCA(x,y)<<endl;
        }
    }
    return 0;
}

ST表

设f[i,j]表示从第i个元素到2^j^个元素的最值

状态转移方程：f[i,j]=max(f[i,j-1],f[i+2^j-1^,j-1])

边界条件：f[i,0]=a[i];

查询：

对于查询区间[L,R]，令x满足2^x^<=R-L+1的最大整数，即x=int(log(R-l+1)/log(2))

Balanced Lineup

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

#include <iostream>
#include <algorithm>
using namespace std;
int f[50010][20];
int g[50010][20];
int main()
{
    int t,n,q,x,y;
    cin>>n>>q;
    for(int i=1;i<=n;i++)
    {
        cin>>t;
        f[i][0]=t;
        g[i][0]=t;
    }
    for(int i=1;(1<<i)<=n;i++)
        for(int j=1;(j+(1<<i)-1)<=n;j++)//j+(1<<i)-1<=n最后一个值要在原数组内
        {
            f[j][i]=max(f[j][i-1],f[j+(1<<(i-1))][i-1]);//2的i次方的区间的最值为前2的i次方-1区间的最值与后2的i次方-1区间最值的最值
            g[j][i]=min(g[j][i-1],g[j+(1<<(i-1))][i-1]);
        }
    while(q--)
    {
        cin>>x>>y;
        int z=0;
        while(1<<(z+1)<=y-x+1)//计算区间长度于2ˆz的关系，用小于2^z<=y-x+1，的 z 把区间分成可以交叉的两部分x 到 x+2^（k）- 1, 到 y -(y-x+1<<k)+1 到 y 的两部分
            z++;
        int ans=max(f[x][z],f[y-(1<<z)+1][z])-min(g[x][z],g[y-(1<<z)+1][z]);
        cout<<ans<<endl;
    }
    return 0;
}

The Tag Game

题解

A代表的是Alice的初始位置，一开始有想BFS，但是如果是B到与A的交叉点的距离比A到与B的交叉点的距离大的时候，那A与B不就不能到达最左边的最远距离，那该怎么解决呢？（本来就不太会BFS,DFS）

我们可以计算两个人到这个数上面的某一个点的距离，如果说Bob到某一个顶点的距离比Alice到某一个点的距离要大的话，这个点不成立，（Bob要尽量把这个时间最大化）！直接比较的是到某一个节点的时候Alice到这个节点的步数是大于Bob到这一点的步数。

注意：就算Bob到最远的角落里，这一点还是要加上的，那么我们只需求Alice到达最远处的距离就行了，然后乘以2.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

#include <iostream>
#include<cstdio>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
const int maxn=2e5+5;
vector<int>mpp[maxn];
int dis1[maxn],dis2[maxn];//分别代表Alice， Bob距离各自初始点的距离
int vis[maxn];//判断是否走过某一点，标记点
int n,x;
void bfs(int beginn,int *num)
{
    queue<int>q;
    memset(num,0,sizeof(num));
    memset(vis,0,sizeof(vis));//标记是否走过
    num[beginn]=0;//距离
    vis[beginn]=1;//标记
    q.push(beginn);
    while(!q.empty())
    {
        int t=q.front();
        q.pop();
        for(int i=0;i<mpp[t].size();i++)
        {
            int l=mpp[t][i];
            if(vis[l]) continue;
            vis[l]=1;
            num[l]=num[t]+1;
            q.push(l);
        }
    }
}
int main()
{
    while(cin>>n>>x)//n-1组数据，Bob初始点
    {
        int a,b;
        for(int i=0;i<maxn;++i)
            mpp[i].clear();
        for(int i=1;i<n;++i)
        {
            cin>>a>>b;
            mpp[a].push_back(b);
            mpp[b].push_back(a);
        }
        bfs(1,dis1);
        bfs(x,dis2);
        int sum=0;
        for(int i=1;i<=n;++i)
        {
            if(dis1[i]>dis2[i])
                sum=max(sum,dis1[i]);
        }
        cout<<sum*2<<endl;
    }
    return 0;
}

A - Coloring a Tree

题解：

先理解题意，给你n个点，代表这一棵树有n个节点。第二行内容是建树的关系。

1
2

例如：1 2 2 1 5
代表：节点2和节点1相连，节点3和节点2相连，节点4和节点2相连，节点5和节点1相连，节点6和节点5相连。

1

第三行内容是需要将各个点涂成的颜色，给这个树涂色，有这么一条原则就是给某一节点涂色，以其为根节点的子树也将变为相应的颜色。

思路：

1
2
3

因为最后需要使所有的点都涂成要求的颜色，一定是按照从根节点到叶子节点遍历的涂色，但所有的点都遍历会造成浪费，我们只需要找出需要涂的点即可，
那么哪些点需要涂呢？我们发现只有那些最后要求的其父亲节点和本身不同色的需要涂色，因为需要向下改变自身颜色，那么只需要统计这样点的个数即可。
最怕dfs因为dfs永远学不会，最后发现也可以直接循环搜索，反正都告诉你子节点父节点关系了，那就循环找呗。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include <iostream>

using namespace std;
int a[10000];
int b[10000];
int main()
{
    int n,count=0;
    cin>>n;
    a[0]=1;a[1]=1;
    for(int i=2;i<=n;i++)
    {
        cin>>a[i];
    }
    for(int i=1;i<=n;i++)
    {
        cin>>b[i];
    }
    for(int i=1;i<=n;i++)
     {
         if(b[i]!=b[a[i]])
         {
             count++;
         }
     }
    cout<<count+1<<endl;
    return 0;
}

Maximum Cost Deletion

You are given a string ss of length nn consisting only of the characters 0 and 1.

You perform the following operation until the string becomes empty: choose some consecutive substring of equal characters, erase it from the string and glue the remaining two parts together (any of them can be empty) in the same order. For example, if you erase the substring 111 from the string 111110, you will get the string 110. When you delete a substring of length ll, you get a⋅l+ba⋅l+b points.

Your task is to calculate the maximum number of points that you can score in total, if you have to make the given string empty.

Input

The first line contains a single integer tt (1≤t≤20001≤t≤2000) — the number of testcases.

The first line of each testcase contains three integers nn, aa and bb (1≤n≤100;−100≤a,b≤1001≤n≤100;−100≤a,b≤100) — the length of the string ss and the parameters aa and bb.

The second line contains the string ss. The string ss consists only of the characters 0 and 1.

Output

For each testcase, print a single integer — the maximum number of points that you can score.

Example

Input

1
2
3
4
5
6
7

3
3 2 0
000
5 -2 5
11001
6 1 -4
100111

Output

1
2
3

6
15
-2

题解：

首先看得分公式a^.^l+b，可知删除几次就需要加几次b，并且a^.^l是固定的，只需要判断b的正负，如果是正数只需要一个一个删除所得的分数必然最大（n^.^a+n^.^b）。如果b是负数，我们需要找到一个数字连续的区域有几块，删除最少连通的数字后再删除一次就可以n^.^a + b^.^( min ( num0 , num1 ) + 1)。

• 例如b<0

• ~~~
  如‘0110001110000110’，
  -> ‘ 0 ’的连通块个数为4
  -> ‘ 1 ’的连通块个数为3
  ->0110001110000110
  ->00001110000110
  ->00000000110
  ->000000000
  ->完

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

  ### 代码 ~~~c++ #include <iostream> using namespace std; char e[1000]; int main() { int num; cin>>num; while(num--) { int n,a,b; cin>>n>>a>>b; cin>>e; int num0=0,num1=0; int flag0 = 0;//寻找最小的连通区域 int flag1 = 0; for(int i = 0;i<n;i++) { if(e[i] == '0') { if(flag0 == 0) { flag0 = 1; flag1 = 0; num0++; } } if(e[i] == '1') { if(flag1 == 0) { flag1 = 1; flag0 = 0; num1++; } } } if(b> 0) cout<<n*(a+b)<<endl; else cout<<b*(min(num0,num1)+1)+n*a<<endl;//注意加1，删除完最少的连通区域，最后还要删除剩下的连通区域 } return 0; }

Secret Passwords

One unknown hacker wants to get the admin’s password of AtForces testing system, to get problems from the next contest. To achieve that, he sneaked into the administrator’s office and stole a piece of paper with a list of nn passwords — strings, consists of small Latin letters.

Hacker went home and started preparing to hack AtForces. He found that the system contains only passwords from the stolen list and that the system determines the equivalence of the passwords a and b as follows:

• two passwords a and b are equivalent if there is a letter, that exists in both a and b;
• two passwords a and b are equivalent if there is a password cc from the list, which is equivalent to both a and b.

If a password is set in the system and an equivalent one is applied to access the system, then the user is accessed into the system.

For example, if the list contain passwords “a”, “b”, “ab”, “d”, then passwords “a”, “b”, “ab” are equivalent to each other, but the password “d” is not equivalent to any other password from list. In other words, if:

• admin’s password is “b”, then you can access to system by using any of this passwords: “a”, “b”, “ab”;
• admin’s password is “d”, then you can access to system by using only “d”.

Only one password from the list is the admin’s password from the testing system. Help hacker to calculate the minimal number of passwords, required to guaranteed access to the system. Keep in mind that the hacker does not know which password is set in the system.

Input

The first line contain integer n(1≤n≤2⋅10) — number of passwords in the list. Next n lines contains passwords from the list – non-empty strings si, with length at most 5050 letters. Some of the passwords may be equal.

It is guaranteed that the total length of all passwords does not exceed 106106 letters. All of them consist only of lowercase Latin letters.

Output

In a single line print the minimal number of passwords, the use of which will allow guaranteed to access the system.

Examples

Input

1
2
3
4
5

4
a
b
ab
d

Output

1

2

Input

1
2
3
4

3
ab
bc
abc

Output

1

1

Input

1
2

1
codeforces

Output

1

1

Note

In the second example hacker need to use any of the passwords to access the system.

题解：

利用并查集，把出现在同一个单词的字母直接合并给一个祖先，然后最后判断有几个祖先即可！

例如：abc和ade；第一个abc是一个集合，祖先是c，第二个因为有a所以他们的祖先都可以传递到e，即a-b-c-d-e。

实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+9;
int n,vis[maxn],pre[maxn],ans;
string a[maxn];
int find(int x){
    int r=x;
    while(pre[r]!=r)
        r=pre[r];
    return r;
}
void join(int q,int w){
     int fx,fy;
    fx=find(q);
    fy=find(w);
    if(fx!=fy)
        pre[fx]=fy;
}
int main()
{
	cin>>n;
	for(int i=0;i<=30;i++)	pre[i]=i;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		int b[27]={0};
		for(int l=a[i].length(),j=0;j<l;j++)
		{
			int s=a[i][j]-'a'+1;//利用ascii码把字母转换为数字
			b[s]++;vis[s]++;//b数组用来判断祖先，vis数组最后用来找祖先
		}
		for(int q=1;q<=26;q++)
		{
			if(b[q]==0)	
                continue;
			for(int j=q+1;j<=26;j++)
			{
				if(b[j]==0)	
                    continue;
				join(q,j);//合并祖先
			}
			break;
		}
	}
	for(int i=1;i<=26;i++)
	if(vis[i]&&find(i)==i)//寻找祖先
        ans++;
	cout<<ans;
}

The Game Of Parity

There are n cities in Westeros. The i-th city is inhabited by ai people. Daenerys and Stannis play the following game: in one single move, a player chooses a certain town and burns it to the ground. Thus all its residents, sadly, die. Stannis starts the game. The game ends when Westeros has exactly k cities left.

The prophecy says that if the total number of surviving residents is even, then Daenerys wins: Stannis gets beheaded, and Daenerys rises on the Iron Throne. If the total number of surviving residents is odd, Stannis wins and everything goes in the completely opposite way.

Lord Petyr Baelish wants to know which candidates to the throne he should support, and therefore he wonders, which one of them has a winning strategy. Answer to this question of Lord Baelish and maybe you will become the next Lord of Harrenholl.

Input

The first line contains two positive space-separated integers, n and k (1 ≤ k ≤ n ≤ 2·105) — the initial number of cities in Westeros and the number of cities at which the game ends.

The second line contains n space-separated positive integers a**i (1 ≤ a**i ≤ 106), which represent the population of each city in Westeros.

Output

Print string “Daenerys” (without the quotes), if Daenerys wins and “Stannis” (without the quotes), if Stannis wins.

Examples

Input

1
2

3 1
1 2 1

Output

1

Stannis

Input

1
2

3 1
2 2 1

Output

1

Daenerys

Input

1
2

6 3
5 20 12 7 14 101

Output

1

Stannis

题解：

1. 如果k==n，直接得出结果。

2. 如果后手能把奇数城毁完，那么后手必胜（因为剩下的，不管怎么毁，总和都为偶数）。

3. 如果后手不能把奇数城毁完

   3.1如果倒数第二步操作的人不能把偶数城毁完，那么最后一步操作的人必胜，因为在最后一步时，既有奇数，也有偶数，可以随意控制输赢。

   3.2如果倒数第二步操作的人能把偶数城毁完，那么剩下的就只有奇数城，所以最后只需看剩下的奇数城有几座，即k。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include<bits/stdc++.h>
using namespace std;
int n, k, a[2];
int main()
{
    cin>>n>>k;
    a[0] = a[1] = 0;
    for(int i = 1; i<=n; i++)
    {
        int x;
        cin>>x;
        a[x%2]++;//输入的人数只需要他的奇偶性，所以用0，1来区分奇偶数
    }
    int winner;
    int step = n-k;
    if(step==0)//n和k一样时，只需要判断奇数城市的个数
        winner = a[1]%2;
    else if(step/2>=a[1])//后手把奇数城全摧毁
        winner=0;
    else
    {
        if(step/2<a[0]) winner = step%2;//判断后手的最后一步是否可以把偶数全摧毁
        else winner = k%2;
    }
    if(winner)
    cout<<"Stannis"<<endl;
    else
        cout<<"Daenerys"<<endl;
}